 A Marshal to Bring Order to the Town of Data Gulch
A Marshal to Bring Order to the Town of Data Gulch
Though not the first, I have been touting the Linked Data Law for a couple of years now [1]. But in a conversation last week, I found that my colleague did not find the premise very clear. I suspect that is due both to cryptic language on my part and the fact no one has really tackled the topic with focus. So, in this post, I try to redress that and also comment on the related role of linked data in the semantic enterprise.
Adding connections to existing information via linked data is a powerful force multiplier, similar to Metcalfe’s law for how the value of a network increases with more users (nodes). I have come to call this the Linked Data Law: the value of a linked data network is proportional to the square of the number of links between data objects.
An early direct mention of the semantic Web and its possible ability to generate network effects comes from a 2003 Mitre report for the government [3]. In it, the authors state, “At present a very small proportion of the data exposed on the web is marked up using Semantic Web vocabularies like RDF and OWL. As more data gets mapped to ontologies, the potential exists to achieve a ‘network effect’.” Prescient, for sure.
In July 2006, both Henry Story and Dion Hinchliffe discussed Metcalfe’s law, with Henry specifically looking to relate it to the semantic Web [4]. He noted that his initial intuition was that “the value of your information grows exponentially with your ability to combine it with new information.” He noted he was trying to find ways to adapt Metcalfe’s law for applicability to the semantic Web.
I picked up on those observations and commented to Henry at that time and in my own post, “The Exponential Driver of Combining Information.” I have been enamoured of the idea ever since, and have begun to weave the idea into my writings.
More recently, in late 2008, James Hendler and Jennifer Golbeck devoted an entire paper to Metcalfe’s law and the semantic Web [5]. In it, they note:
“This linking between ontologies, and between instances in documents that refer to terms in another ontology, is where much of the latent value of the Semantic Web lies. The vocabularies, and particularly linked vocabularies using URIs, of the Semantic Web create a graph space with the ability to link any term to any other. As this link space grows with the use of RDF and OWL, Metcalfe’s law will once again be exploited – the more terms to link to, and the more links created, the more value in creating more terms and linking them in.”
A Refresher on Metcalfe’s Law
Metcalfe’s law states that the value of a telecommunications network is proportional to the square of the number of users of the system (n²) (note: it is not exponential, as some of the points above imply). Robert Metcalfe formulated it about 1980 in relation to Ethernet and fax machines; the “law” was then named for Metcalfe and popularized by George Gilder in 1993.
These attempts to estimate the value of physical networks were in keeping with earlier efforts to estimate the value of a broadcast network. That value is almost universally agreed to be proportional to the number of users, as accepted as Sarnoff’s law (see further below).
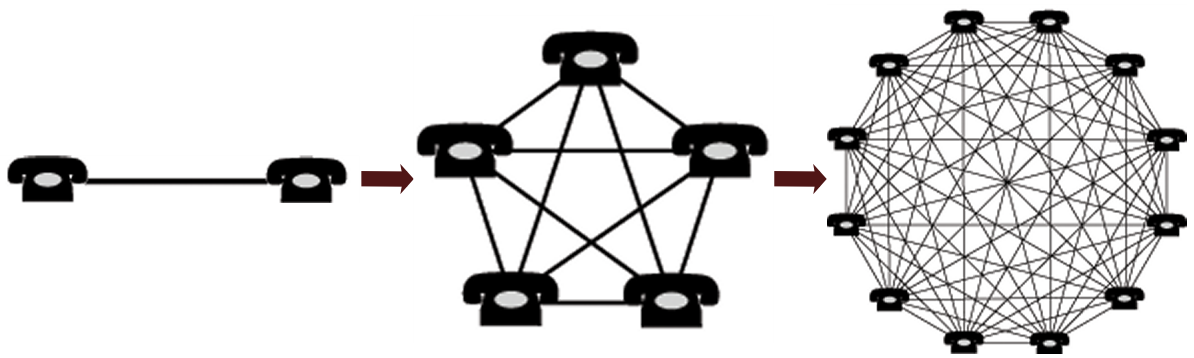
The actual algorithm proposed by Metcalfe calculates the number of unique connections in a network with n nodes to be n(n − 1)/2, which is proportional to n2. This makes Metcalfe’s law a quadratic growth equation.
As nodes get added, then, we see the following increase in connections:
This diagram, modified from Wikipedia to be a horizontal image, shows how two telephones can make only one connection, five can make 10 connections, and twelve can make 66 connections, etc.
By definition, a physical network is a connected network. Thus, every time a new node is added to the network, connections are added, too. This general formula has also been embraced as a way to discuss social connections on the Internet [6].
Analogies to Linked Data
Like physical networks, the interconnectedness of the semantic Web or semantic enterprise is a graph.
The idea behind linked data is to make connections between data. Unlike physical telecommunication networks, however, the nodes in the form of datasets and data are (largely) already there. What is missing are the connections. The build-out and growth that produces the network effects in a linked data context do not result from adding more nodes, but from the linking or connecting of existing nodes.
The fact that adding a node to a physical network carries with it an associated connection has tended to conjoin these two complementary requirements of node and connection. But, to grok the real dynamics and to gain network effects, we need to realize: Both nodes and connections are necessary.
One circumstance of the enterprise is that data nodes are everywhere. The fact that the overwhelming majority are unconnected is why we have adopted the popular colloquialism of data “silos”. There are also massive amounts of unconnected data on the Web in the form of dynamic databases only accessible via search form, and isolated data tables and listings virtually everywhere.
Thus, the essence of the semantic enterprise and the semantic Web is no more complicated than connecting — meaningfully — data nodes that already exist.
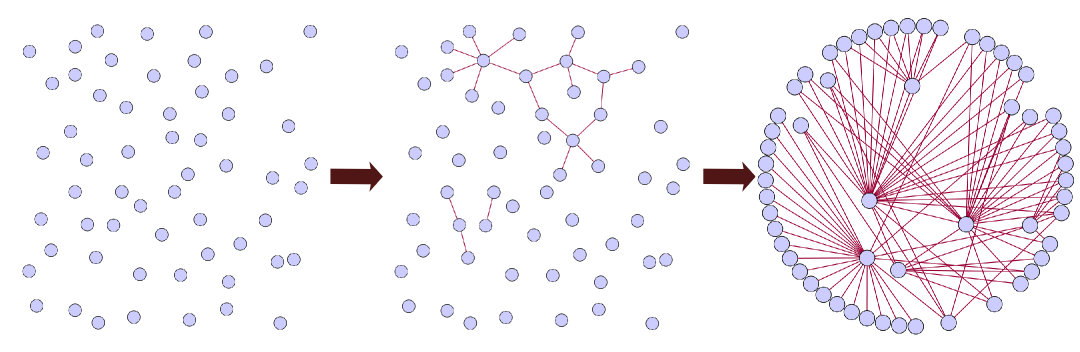
As the following diagram shows, unconnected data nodes or silos look like random particles caught in the chaos of Brownian motion:
As initial connections get made, bits of structure begin to emerge. But, as connections are proliferated — exactly equivalant to the network effects of connected networks — coherence and value emerge.
Look at the last part in the series diagram above. We not only see that the same nodes are now all connected, with the inferences and relationships that result from those connections, but we can also see entirely new structures emerge by virtue of those connections. All of this structure and meaning was totally absent prior to making the linked data connections.
Quantifying the Network Effect
So, what is the benefit of this linked data? It depends on the product of the value of the connections and the multiplier of the network effect:
Just as it is hard to have a conversation via phone with yourself, or to collaborate with yourself, the ability to gain perspective and context from data comes from connections. But like some phone calls or some collaborations, the value depends on the participants. In the case of linked data, that depends on the quality of the data and its coherence [7]. The value “constant” for connected linked data depends in some manner on these factors, as well as the purposes and circumstances to which that linked data might be applied.
Even in physical networks or social collaboration contexts, the “value” of the network has been hard to quantify. And, while academics and researchers will appropriately and naturally call for more research on these questions, we do not need to be so timid. Whatever the alpha constant is for quantifying the value of a linked data network, our intuition should be clear that making connections, finding relationships, making inferences, and making discoveries can not occur when data is in isolation.
Because I am an advocate, I believe this alpha constant of value to be quite large. I believe this constant is also higher for circumstances of business intelligence, knowledge management and discovery.
The second part of the benefit equation is the multiplier for network effects. We’ve mentioned before the linear growth advantage due to broadcast networks (Sarnoff law) and the standard quadratic growth assumption of physical and social networks (Metcalfe law). Naturally, there have been other estimates and advocacies.
David Reed [8], for example, also adds group effects and has asserted an exponential multiplier to the network effect (like Henry Story’s initial intuition noted above). As he states,
“[E]ven Metcalfe’s Law understates the value created by a group-forming network [GFN] as it grows. Let’s say you have a GFN with n members. If you add up all the potential two-person groups, three-person groups, and so on that those members could form, the number of possible groups equals 2n. So the value of a GFN increases exponentially, in proportion to 2n. I call that Reed’s Law. And its implications are profound.”
Yet not all agree with the assertion of an exponential multiplier, let alone the quadratic one of Metcalfe. Odlyzko and Tilly [9] note that Metcalfe’s law would hold if the value that an individual gets personally from a network is directly proportional to the number of people in that network. But, then they argue that does not hold because of local preferences or different qualities of interaction. In a linked data context, such arguments have merit, though you may also want to see Metcalfe’s own counter-arguments [6].
Hinchliffe’s earlier commentary [4] provided a nice graphic that shows the implications of these various multiplers on the network effect, as a function of nodes in a network:
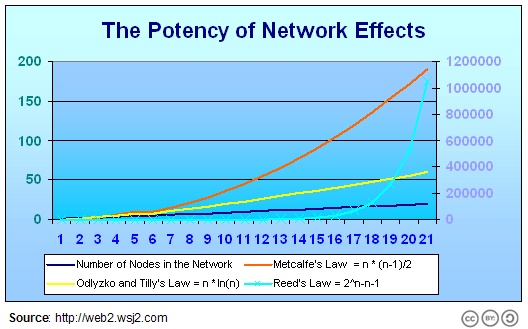
Various Estimates for the ‘Network Effect’
I believe we can dismiss the lower linear bound of this question and likely the higher exponential one as well (that is, Reed’s law, because quality and relevance questions make some linked data connections less valuable than others). Per the above, that would suggest that the multiplier of the linked data network is perhaps closer to the Metcalfe estimate or similar.
In any event, it is also essential to point out that connecting data indiscriminantly for linked data’s sake will likely deliver few, if any, benefits. Connections must still be coherent and logical for the value benefits to be realized.
The Role and Contribution of Linked Data
I elsewhere discuss the role of linked data in the enterprise and will continue to do so. But, there are some implications in the above that warrant some further observations.
It should be clear that the graph and network basis of linked data, not to mention some of the uncertainties as to quantifying benefits, suggests the practice should be considered apart from mission-critical or transactional uses in the enterprise. That may change with time and experience.
There are also open questions about data quality in terms of inputs to linked data and possible erroneous semantics and ontologies to guide the linked connections. Operational uses should be kept off the table for now. Like physical networks, not all links perform well and not all have usefulness. Similarly to how poor connections may be encountered in physical networks, they should be either taken off-ledger or relegated to a back-up basis. Linked data should be understood and treated no differently than networks of variable quality.
Such realism is important — for both internal and external linked data advocates — to allow linked data to be applied in the right venues at acceptable risk and with likely demonstrable benefits. Elsewhere I have advocated an approach that builds on existing assets; here I advocate a clear and smart understanding of where linked data can best deliver network effects in the near term.
And, so, in the nearest term, enterprise applications that best fit linked data promises and uncertainties include:
- Establishing frameworks for data federation
- Business intelligence
- Discovery
- Knowledge management and knowledge resources
- Reasoning and inference
- Development of internal common language
- Learning and adopting data-driven apps [10], and
- Staging and analysis for data cleaning.
A New Deputy Has Come to Town
As in the Wild West, the new deputy marshal and his tin badge did not guarantee prosperity. But a good marshal would deliver law and order. And those are the preconditions for the town folk to take charge of building their own prosperity.
Linked data is a practice for starting to bring order and connections to your existing data. Once some order has been imposed, the framework then becomes a basis for defining meanings and then gaining value from those connections.
Once order has been gained, it is up to the good citizens of Data Gulch to then deliver the prosperity. Broad participation and the network effect are one way to promote that aim. But success and prosperity still depends on intelligence and good policies and practice.





I’ve been thinking about what exactly it would be that result in a network effect for Linked Data; I’ve concluded that there can be both normal and inverse network effects, depending on the specific application.
As I sat there this morning listening to a presentation on XBRL I could not help thinking that those pushing XBRL are not committed to the same vision of linked data. In many respects companies are being required (in some countries through legislation) to prpvode financial information marked up in XBRL. However I see little evidence to suggest that there is any relaisation or real interest amongst this community in the real merits of linked data ie the multiplier effect.