 Knowledge Representation Guidelines from Charles S. Peirce
Knowledge Representation Guidelines from Charles S. Peirce
‘Representation’ is the second half of knowledge representation (KR), the field of artificial intelligence dedicated to representing information about the world in a form that a computer system can utilize to solve complex tasks. One dictionary sense is that ‘representation’ is the act of speaking or acting on behalf of someone else; this is the sense, say, of a legislative representative. Another sense is a statement made to some formal authority communicating an assertion, opinion or protest, such as a notarized document. The sense applicable to KR, however, according to the Oxford Dictionary of English, is one of ‘re-presenting’. That is, “the description or portrayal of someone or something in a particular way or as being of a certain nature” [1]. In this article I investigate this sense of ‘re-presenting’ following the sign-making guidelines of Charles Sanders Peirce [2] [3] (which we rely upon in our KBpedia knowledge structure).
When we see something, or point to something, or describe something in words, or think of something, we are, of course, using proxies in some manner for the actual thing. If the something is a ‘toucan’ bird, that bird does not actually reside in our head when we think of it. The ‘it’ of the toucan is a ‘re-presentation’ of the real, dynamic toucan. The representation of something is never the actual something, but is itself another thing that conveys to us the idea of the real something. In our daily thinking we rarely make this distinction, thankfully, otherwise our flow of thoughts would be completely jangled. Nonetheless the distinction is real, and when inspecting the nature of knowledge representation, needs to be consciously considered.
How we ‘re-present’ something is also not uniform or consistent. For the toucan bird, perhaps we make caw-caw bird noises or flap our arms to indicate we are referring to a bird. Perhaps we simply point at the bird. Or, perhaps we show a picture of a toucan or read or say aloud the word “toucan” or see the word embedded in a sentence or paragraph, as in this one, that also provides additional context. How quickly or accurately we grasp the idea of toucan is partly a function of how closely associated one of these signs may be to the idea of toucan bird. Probably all of us would agree that arm flapping is not nearly as useful as a movie of a toucan in flight or seeing one scolding from a tree branch.
The question of what we know and how we know it fascinated Peirce over the course of his intellectual life. He probed this relationship between the real or actual thing, the object, with how that thing is represented and understood. This triadic relationship between object, representation and interpretation forms a sign, and is the basis for the process of sign-making and understanding, which Peirce called semiosis [4]. Peirce’s basic sign relationship is central to his own epistemology and resides at the core of how we use knowledge representation in KBpedia.
The Shadowy Object
Yet even the idea of the object, in this case the toucan bird, is not necessarily so simple. There is the real thing itself, the toucan bird, with all of its characters and attributes. But how do we ‘know’ this real thing? Bees, like many insects, may perceive different coloration for the toucan and adjacent flowers because they can see in the ultraviolet spectrum, while we do not. On the other hand, most mammals in the rain forest would also not perceive the reds and oranges of the toucan’s feathers, which we readily see. Perhaps only fellow toucans could perceive by gestures and actions whether the object toucan is healthy, happy or sad (in the toucan way). Humans, through our ingenuity, may create devices or technologies that expand our standard sensory capabilities to make up for some of these perceptual gaps, but technology will never make our knowledge fully complete. Given limits to perceptions and the information we have on hand, we can never completely capture the nature of the dynamic object, the real toucan bird.
Then, of course, whatever representation we have for the toucan is also incomplete, be it a mental image, a written description, or a visual image (again, subject to the capabilities of our perceptions). We can point at the bird and say “toucan”, but the immediate object that it represents still is different than the real object. Or, let’s take another example more in keeping with the symbolic nature of KR, in this case the word for ‘bank’. We can see this word, and if we speak English, even recognize it, but what does this symbol mean? A financial institution? The shore of a river? Turning an airplane? A kind of pool shot? Tending a fire for the evening? In all of these examples, there is an actual object that is the focus of attention. But what we ‘know’ about this object depends on what we perceive or understand and who or what is doing the perceiving and the understanding. We can never fully ‘know’ the object because we can never encompass all perspectives and interpretations.
Peirce well recognized these distinctions. He termed the object of our representations the immediate object, while also acknowledging this representation is not fully capturing of the underlying, real dynamical object:
“Every cognition involves something represented, or that of which we are conscious, and some action or passion of the self whereby it becomes represented. The former shall be termed the objective, the latter the subjective, element of the cognition. The cognition itself is an intuition of its objective element, which may therefore be called, also, the immediate object.” (CP 5.238)
“Namely, we have to distinguish the Immediate Object, which is the Object as the Sign itself represents it, and whose Being is thus dependent upon the Representation of it in the Sign, from the Dynamical Object, which is the Reality which by some means contrives to determine the Sign to its Representation.” (CP 4.536)
“As to the Object, that may mean the Object as cognized in the Sign and therefore an Idea, or it may be the Object as it is regardless of any particular aspect of it, the Object in such relations as unlimited and final study would show it to be. The former I call the Immediate Object, the latter the Dynamical Object.” (CP 8.183)
Still, we can not know anything without the sign process. One imperative of knowledge representation — within reasonable limits of time, resources and understanding — is to try to ensure that our immediate representation of the objects of our discourse are in as close a correspondence to the dynamic object as possible. This imperative, of course, does not mean assembling every minute bit of information possible in order to characterize our knowledge spaces. Rather, we need to seek a balance between what and how we characterize the instances in our domains with the questions we are trying to address, all within limited time and budgets. Peirce’s pragmatism, as expressed through his pragmatic maxim, helps provide guidance to reach this balance.
Three Modes of Representation
Representations are signs (CP 8.191), and the means by which we point to, draw or direct attention to, or designate, denote or describe a particular object, entity, event, type or general. A representational relationship has the form of re:A. Representations can be designative of the subject, that is, be icons or symbols (including labels, definitions, and descriptions). Representations may be indexes that more-or-less help situate or provide traceable reference to the subject. Or, representations may be associations, resemblances and likelihoods in relation to the subject, more often of indeterminate character.
In Peirce’s mature theory of signs, he characterizes signs according to different typologies, which I discuss further in the next section. One of his better known typologies is how we may denote the object, which, unlike some of his other typologies, he kept fairly constant throughout his life. Peirce formally splits these denotative representations into three kinds: icons, indexes, or symbols (CP 2.228, CP 2.229 and CP 5.473).
“. . . there are three kinds of signs which are all indispensable in all reasoning; the first is the diagrammatic sign or icon, which exhibits a similarity or analogy to the subject of discourse; the second is the index, which like a pronoun demonstrative or relative, forces the attention to the particular object intended without describing it; the third [or symbol] is the general name or description which signifies its object by means of an association of ideas or habitual connection between the name and the character signified.” (CP 1.369)
The icon, which may also be known as a likeness or semblance, has a quality shared with the object such that it resembles or imitates it. Portraits, logos, diagrams, and metaphors all have an iconic denotation. Algebraic expressions are also viewed by Peirce as icons, since he believed (and did much to prove) that mathematical operations can be expressed through diagrammatic means (as is the case with his later existential graphs).
An index denotes the object by some form of linkage or connection. An index draws or compels attention to the object by virtue of this factual connection, and does not require any interpretation or assertion about the nature of the object. A pointed finger to an object or a weathervane indicating which direction the wind is blowing are indexes, as are keys in database tables or Web addresses (URIs or URLs [5]) on the Internet. Pronouns, proper names, and figure legends are also indexes.
Symbols, the third kind of denotation, represent the object by virtue of accepted conventions or ‘laws’ or ‘habits’ (Peirce’s preferred terms). There is an understood interpretation, gained through communication and social consensus. All words are symbols, plus their combinations into sentences and paragraphs. All symbols are generals, but which need to be expressed as individual instances or tokens. For example, ‘the’ is a single symbol (type), but it is expressed many times (tokens) on this page. Knowledge representation, by definition, is based on symbols, which need to be interpreted by either humans or machines based on the conventions and shared understandings we have given them.
Peirce confined the word representation to the operation of a sign or its relation to the interpreter for an object. The three possible modes of denotation — that is, icon, index or symbol — Peirce collectively termed the representamen:
“A very broad and important class of triadic characters [consists of] representations. A representation is that character of a thing by virtue of which, for the production of a certain mental effect, it may stand in place of another thing. The thing having this character I term a representamen, the mental effect, or thought, its interpretant, the thing for which it stands, its object.” (CP 1.564)
Peirce’s Semiosis and Triadomany
A core of Peirce’s world view is thus based in semiotics, the study and logic of signs. In a seminal writing, “What is in a Sign?” [6], Peirce wrote that “every intellectual operation involves a triad of symbols” and “all reasoning is an interpretation of signs of some kind.” This basic triad representation has been used in many contexts, with various replacements or terms at the nodes. One basic form is known as the Meaning Triangle, popularized by Ogden and Richards in 1923 [7], surely reflective of Peirce’s ideas.
For Peirce, the appearance of a sign starts with the representamen, which is the trigger for a mental image (by the interpretant) of the object. The object is the referent of the representamen sign. None of the possible bilateral (or dyadic) relations of these three elements, even combined, can produce this unique triadic perspective. A sign can not be decomposed into something more primitive while retaining its meaning.
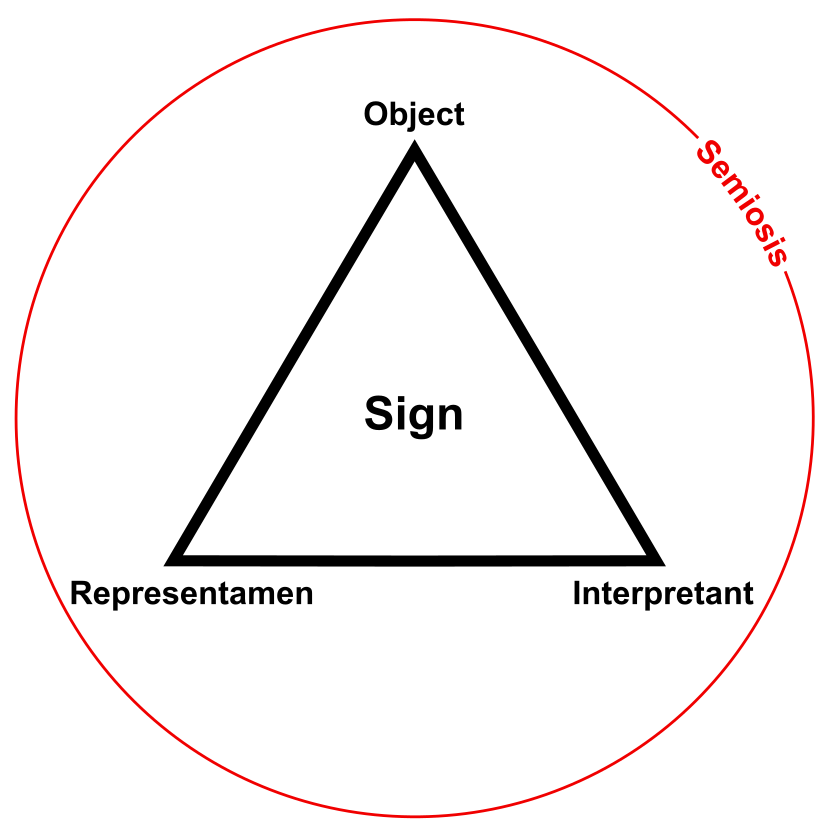
Figure 1: The Object-Representamen-Interpretant Sign Process (Semiosis)
Let’s summarize the interaction of these three sign components [8]. The object is the actual thing. It is what it is. Then, we have the way that thing is conveyed or represented, the representamen, which is an icon, index or symbol. Then we have how an agent or the perceiver of the sign understands and interprets the sign, the interpretant, which in its barest form is a sign’s meaning, implication, or ramification. For a sign to be effective, it must represent an object in such a way that it is understood and used again. Basic signs can be building blocks for still more complex signs, such as words combined into sentences. This makes the assignment and use of signs a community process of understanding and acceptance [9], as well as a truth-verifying exercise of testing and confirming accepted associations (such as the meanings of words or symbols).
Complete truth is the limit where the understanding of the object by the interpretant via the sign is precise and accurate. Since this limit is never achieved, sign-making and understanding is a continuous endeavor. The overall process of testing and refining signs so as to bring understanding to a more accurate understanding is what Peirce meant by semiosis. Peirce’s logic of signs in fact is a taxonomy of sign relations, in which signs get reified and expanded via still further signs, ultimately leading to communication, understanding and an approximation of canonical truth. Peirce saw the scientific method as an exemplar of this process.
The understanding of the sign is subject to the contexts for the object and agent and the capabilities of the interpreting agent; that makes the interpretant an integral component of the sign. Two different interpretants can derive different meanings from the same representation, and a given object may be represented by different tokens. When the interpretant is a human and the signs are language, shared understandings arise from the meanings given to language by the community, which can then test and add to the truth statements regarding the object and its signs, including the usefulness of those signs. Again, these are drivers to Peirce’s semiotic process.
In the same early 1867 paper in which Peirce laid out the three modes of denotation of icon, index, and symbol [10] [11], he also presented his three phenomenological categories for the first time, what I (and others) have come to call his universal categories of Firstness, Secondness and Thirdness. This seminal paper also provides the contextual embedding of these categories, which is worth repeating in full:
“The five conceptions thus obtained, for reasons which will be sufficiently obvious, may be termed categories. That is,
BEING,
Quality (reference to a ground),
Relation (reference to a correlate),
Representation (reference to an interpretant),
SUBSTANCE.
The three intermediate conceptions may be termed accidents.” (EP 1:6, CP 1.55)
Note the commas, suggesting the order, and the period, in the listing. In his later writings, Peirce ceases to discuss Being and Substance directly, instead focusing on the ‘accidental’ categories that became the first expression of his universal categories. Being, however, represents all that there is and is the absolute, most abstract starting point for Peirce’s epistemology. The three ‘accidental’ categories of Quality, Relation and Representation are one of the first expressions of Peirce’s universal categories or Firstness, Secondness and Thirdness as applied to Substance. “Thus substance and being are the beginning and end of all conception. Substance is inapplicable to a predicate, and being is equally so to a subject.” (CP 1.548)
These two, early triadic relations — one, the denotations in signs, and, two, the universal categories — are examples of Peirce’s lifelong fascination with trichotomies [12]. He used triadic thinking in dozens of areas in his various investigations, often in a recursive manner (threes of threes). It is not surprising, then, that Peirce also applied this mindset to the general characterization of signs themselves.
Peirce returned to the idea of sign typologies and notations at the time of his Lowell Institute lectures at Harvard in 1903 [13]. Besides the denotations of icons, indexes and symbols, that he retained, and represent the three different ways to denote an object, Peirce also proffered three ways to describe the signs themselves (representamen) to fulfill different purposes, and three ways to interpret signs (interpretant) based on possibility, fact, or reason. This more refined view of three trichotomies should theoretically result in 27 different sign possibilities (3 x 3 x 3), except the nature of the monadic, dyadic and triadic relationships embedded in these trichotomies only logically leads to 10 variants (1 + 3 + 6) [14].
Peirce split the purposes (uses) of signs into qualisigns (also called tones, potisigns, or marks), which are signs that consists in a quality of feeling or possibility, and are in Firstness; into sinsigns (also called tokens or actisigns), which consist in action/reaction or actual single occurrences or facts, and are in Secondness; or legisigns (also called types or famisigns), which are signs that consist of generals or representational relations, and are in Thirdness. Instances (tokens) of legisigns are replicas, and thus are a sinsign. All symbols are legisigns. Synonyms, for example, are replicas of the same legisign, since they mean the same thing, but are different sinsigns.
Peirce split the interpretation of signs into three categories. A rheme (also called sumisign or seme) is a sign that stands for its object for some purpose, expressed as a character or a mark. Terms are rhemes, but they also may be icons or indexes. Rhemes may be diagrams, proper nouns or common nouns. A proposition expressed with its subject as a blank (unspecified) is also a rheme. A dicisign (also called dicent sign or pheme ) is the second type of sign, that of actual existence. Icons can not be dicisigns. Dicisigns may be either indexes or symbols, and provide indicators or pointers to the object. Standard propositions or assertions are dicisigns. And an argument (also called suadisign or delome) is the third type of sign that stands for the object as a generality, as a law or habit. A sign itself is an argument, including major and minor premises and conclusions. Combinations of assertions or statements, such as novels or works of art, are arguments.
Table 1 summarizes these 10 sign types and provides some examples of how to understand them:
|
Sign by use |
Relative
to
object |
Relative
to
interpretant |
Sign name (redundancies) |
Some examples |
| I |
Qualisign |
Icon |
Rheme |
(Rhematic Iconic) Qualisign |
A feeling of “red” |
| II |
Sinsign |
Icon |
Rheme |
(Rhematic) Iconic Sinsign |
An individual diagram |
| III |
Index |
Rheme |
Rhematic Indexical Sinsign |
A spontaneous cry |
| IV |
Dicisign |
Dicent (Indexical) Sinsign |
A weathercock or photograph |
| V |
Legisign |
Icon |
Rheme |
(Rhematic) Iconic Legisign |
A diagram, apart from its factual individuality |
| VI |
Index |
Rheme |
Rhematic Indexical Legisign |
A demonstrative pronoun |
| VII |
Dicisign |
Dicent Indexical Legisign |
A street cry (identifying the individual by tone, theme) |
| VIII |
Symbol |
Rheme |
Rhematic Symbol (Legisign) |
A common noun |
| IX |
Dicisign |
Dicent Symbol (Legisign) |
A proposition (in the conventional sense) |
| X |
Argument |
Argument (Symbolic Legisign) |
A syllogism |
Table 1: Ten Classifications of Signs [15]
This schema is the last one fully developed by Peirce. However, in his last years, he also developed 28-class and 66-class sign typologies, though incomplete in important ways and details. These expansions reflected sign elaborations for various sub-classes of Peirce’s more mature trichotomies, such as for the immediate and dynamic objects previously discussed (see CP 8.342-379). There is a symmetry and recursive beauty to these incomplete efforts, with sufficient methodology suggested to enable informed speculations as to where Peirce may have been heading [16] [17] [18] [19].
We have taken a different path with KBpedia. Rather than engage in archeology, we have chosen to try to fathom and plumb Peirce’s mindset, and then apply that mindset to the modern challenge of knowledge representation. Peirce’s explication of the centrality and power of signs, his fierce belief in logic and reality, and his commitment to discover the fundamental roots of episteme, have convinced us there is a way to think about Peirce’s insights into knowledge representation attuned to today. Peirce’s triadomany [12], especially as expressed through the universal categories, provides this insight.
[2] Charles S. Peirce (1839 – 1914), pronounced “purse,” was an American logician, scientist, mathematician, and philosopher of the first rank. Peirce is a major guiding influence for our KBpedia knowledge system. Quotes in the article are mostly from the electronic edition of
The Collected Papers of Charles Sanders Peirce, reproducing Vols. I-VI, Charles Hartshorne and Paul Weiss, eds., 1931-1935, Harvard University Press, Cambridge, Mass., and Arthur W. Burks, ed., 1958, Vols. VII-VIII, Harvard University Press, Cambridge, Mass. The citation scheme is volume number using Arabic numerals followed by section number from the collected papers, shown as, for example, CP 1.208.
[3] Some material in this article was drawn from my prior articles at the
AI3:::Adaptive Information blog: “Give Me a Sign: What Do Things Mean on the Semantic Web?” (Jan 2012); “A Foundational Mindset: Firstness, Secondness, Thirdness” (March 2016); “The Irreducible Truth of Threes” (Sep 2016); “Being Informed by Peirce” (Feb 2017). For all of my articles about Peirce, see
https://www.mkbergman.com/category/c-s-peirce/.
[4] Peirce actually spelled it “
semeiosis”. While it is true that other philosophers such as Ferdinand de Saussure also employed the shorter term “semiosis”, I also use this more common term due to greater familiarity.
[5] The URI “sign” is best seen as an
index: the URI is a pointer to a representation of some form, be it electronic or otherwise. This representation bears a relation to the actual thing that this referent represents, as is true for all triadic sign relationships. However, in some contexts, again in keeping with additional signs interpreting signs in other roles, the URI “sign” may also play the role of a symbolic “name” or even as a signal that the resource can be downloaded or accessed in electronic form. In other words, by virtue of the conventions that we choose to assign to our signs, we can supply additional information that augments our understanding of what the URI is, what it means, and how it is accessed.
[7] C.K. Ogden and I. A. Richards. 1923.
The Meaning of Meaning. Harcourt, Brace, and World, New York.
[8] Peirce himself sometimes used a Y-shaped figure. The triangle is simpler to draw and in keeping with the familiar Ogden and Richards figure of 1923.
[10] Charles S. Peirce. 1867. “On a New List of Categories”. In
Proceedings of the American Academy of Arts and Sciences.
[11] Among all of his writings, Peirce said “The truth is that my paper of 1867 was perhaps the least unsatisfactory, from a logical point of view, that I ever succeeded in producing; and for a long time most of the modifications I attempted of it only led me further wrong.” (CP 2.340).
[12] See CP 1.568, wherein Peirce provides “The author’s response to the anticipated suspicion that he attaches a superstitious or fanciful importance to the number three, and forces divisions to a Procrustean bed of trichotomy.”
[13] Charles S. Peirce and The Peirce Edition Project. 1998. “Nomenclature and Divisions of Triadic Relations, as Far as They Are Determined”. In
The Essential Peirce: Selected Philosophical Writings, Volume 2 (1893-1913). Indiana University Press, Bloomington, Indiana, 289–299.
[14] Understand each trichotomy is comprised of three elements, A, B and C. The monadic relations are a singleton, A, which can only match with itself and A variants. The dyadic relations can only be between A and B and derivatives. And the triadic relations are between all variants and derivatives. Thus, the ten logical combinations for the three trichotomies are: A-A’-A’’; B-A’-A’’; B-B’-A’’; B-B’-B’’; C-A’-A’’; C-B’-A’’; C-B’-B’’; C-C’-A’’; C-C’-B’’; and C-C’-C’’, for a total of ten options.
[15] From CP 2.254-263, EP 2:294-296, and MS 540 of 1903.
[18] P. Farias and J. Queiroz. 2003. “On Diagrams for Peirce’s 10, 28, and 66 Classes of Signs”.
Semiotica 147, 1/4: 165–184.
[19] Tony Jappy. 2017.
Peirce’s Twenty-Eight Classes of Signs and the Philosophy of Representation: Rhetoric, Interpretation and Hexadic Semiosis. Bloomsbury Academic. Retrieved September 29, 2017 from
http://www.oapen.org/search?identifier=625766.
 A Major Milestone in Semantic Technologies and AI After a Decade of Effort
A Major Milestone in Semantic Technologies and AI After a Decade of Effort

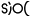



 More Active Tools than Last Census
More Active Tools than Last Census
 Knowledge Representation Guidelines from Charles S. Peirce
Knowledge Representation Guidelines from Charles S. Peirce